Netflix是美国一家提供在线电影租赁服务的公司,用户对Netflix上的电影提供评分(1-5),分数越高表示用户对相应电影的评价越高。Netflix的推荐系统Cinematch对这些积累的电影评分数据进行分析,学习用户的兴趣偏好,为用户推荐一些感兴趣的电影。2006年,Netflix建立了Netflix Prize推荐竞赛,目标是实现高效的推荐系统,推荐效果是在Cinematch的基础上改进10%。
本博文对Netflix推荐大赛的特等奖( Grand Prize)得主BellKor’s Pragmatic Chaos(BPC)团队的解决方案做详细的介绍,主要包括Netflix数据集、系统设计、以及推荐方案。
1.Netflix Prize数据集
使用6年(2000-2005)的电影评分数据,测试集100,000,000的评分,480,000个用户,17,770部电影。测试集取其中的一部分评分数据(2,800,000)。
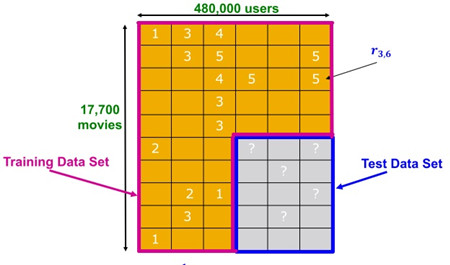
用户给电影的评分通常为显式信息或者显式评分,但在实际业务场景中还包括一些隐式信息,如电商场景中的浏览、购买、收藏等行为,Netflix数据集中并没有给出类似于上述行为的隐式信息。
数据集特点
- 稀疏性:接近99%的评分未知;
- 长尾性:大部分用户只对极少的电影进行了评分;大部分电影只收到极少的用户评分;
2. 推荐效果评估
使用均方根误差(RMSE)作为推荐效果的评估标准。
\[ RMSE = \frac {1} {R} \sqrt{\sum_{(i,x)\in R} (\hat{r_{xi}} - r_{xi})^2 } \]
其中,\(r_{xi}\)为用户x在电影i上的实际评分,\(\hat{r}_{xi}\)为据测评分。
3.BellKor推荐系统
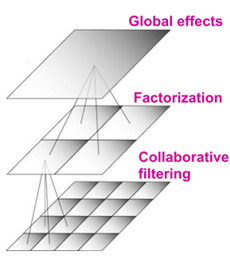
BellKor推荐系统采用多级数据建模:结合从最顶层、区域到局部的方式建模。
-
全局作用(Global Effects):Global Effects是为了消除全局用户或电影单方面对评分的影响,为学习用户与电影之间相互作用的协同过滤模型净化评分。
-
矩阵分解(Matrix Factorization:为了克服协同过滤问题中已知评分的稀疏性,降低模型的过度拟合,矩阵分解将原始稀疏的评分矩阵分解为两个稠密的因子矩阵,因子矩阵用来表达“区域影响”,如电影类型、用户口味等。
-
协同过滤(Collaborative Filtering):协同过滤用来学习用户与电影之间局部相互作用。
3.1 基准预测模型(Baseline Predictor, BP)
全局作用模型(Global Effects)和基准预测模型都属于评分预处理的方法,是为了消除数据中掩盖真实信息的噪音,对数据净化。全局作用模型和基准预测模型描述了用户对电影评分所体现出来的各种趋势。本博文主要对基准预测模型做详细介绍,全局作用模型请查阅相关资料。
协同过滤模型一般通过学习用户与产品之间的相互作用获得最终的预测评分。但是除了用户和电影的相互作用外,电影评分还受其他因素的影响,如有些用户对电影的评分普遍偏高,4分是基准;而另外一些用户对电影的评分普遍偏低,2分是基准。同样,有些电影由于剧情、演员等因素比其他电影更偏向获得高分。另外,用户的心情、环境以及体验等诸多因素都影响着电影评分。基准预测模型就是要找到不能由相互作用所解释的那部分规律或者趋势。

模型1:引入用户偏差和电影偏差
\[ b_{xi} = \mu + b_x + b_i \]
其中,\(b_{xi}\)为电影评分\(r_{xi}\)的基准预测评分,\(\mu\)为全局评分均值(overall mean),\(b_x\)代表用户x的评分偏差,\(b_i\)代表电影i获得的评分偏差。如:假设全局评分均值\(\mu = 3.7\),Joe的评分倾向比平均评分低0.2分,电影The Six Sense获得评分倾向比平均高0.5分,所以Joe对电影The Six Sense的基准预测评分为3.7 + 0.5 - 0.2 = 4。
模型2:引入时间
用户对电影的理解可能因为他最近看了其他电影,如一个用户对战狼2的电影特别感兴趣,这部电影也会让用户掀起对同类电影的好感,对吴京早期的战狼1更加关注。模型1推广为如下形式: \[ b_{xi} = \mu + b_x(t_{xi}) + b_i(t_{xi}) \] 其中,\(b_x(t_{xi})\)和\(b_i(t_{xi})\)为关于时间变化的函数。一般地,电影的变化程度往往需要较长的时间才能表现出来,对于电影偏差,可以通过对时间进行分段处理,然后在每段中使用相同的偏差值。划分的段数越多,对电影偏差描述就也精确,但是每段中的数据越少,估计出的值也越不准确。在比赛具体的实现中,每段的时间大约对应连续的10周,整个时间分成30段。电影偏差为: \[ b_i(t) = b_i + b_{i,Bin(t)} \] \(Bin(t)\)把时间映射到[1,30]。
相对于电影,用户对电影的评分在短期内变化很大,如用户可能今天心情好,对看过的所有的电影都打了高分,有一天失恋了,他可能后悔给这些电影高分。为了简单期间,用如下时间偏差这个线性函数获得用户偏差随时间变化的作用。用户在时间t对电影进行了评分,那么这个评分的时间偏差为:
\[ dev_x(t) = sign(t - t_x) * |t - \bar{t_x}|^{\beta} \]
\(|t - \bar{t_x}|\)为时间\(t\)和\(\bar{t_x}\)之间相差的天数,\(\beta\)通过交叉验证或者超参数学习方法学习得到,在实现中选\(\beta = 0.4\)。那么,第一个随时间变化的用户偏差如下:
\[ b_x^{(1)}(t) = b_x + \alpha_{x} * dev_x(t) \]
其中,\(b_x\)和\(\alpha_{x}\)模型学习参数。
上面的函数反映了用户偏差随时间变化的作用,但是一个用户在很短的时间内偏差可能会发生很大的变化。在Netflix数据集中发现,一个用户在一天内的评分倾向于某个值附近。第二个用户偏差描述了用户单日内的评分趋势:
\[ b_x^{(2)}(t) = b_x + b_{xt} \]
其中,\(b_x\)和\(b_{xt}\)模型学习参数。
综合单日变化和持续变化这两种作用,得到加强的电影偏差:
\[ b_x^{(1)}(t) = b_x + \alpha_{x} * dev_x(t) + b_{xt} \]
综合电影偏差和用户偏差,得到模型2的基准预测评分:
\[ b_{xi} = \mu + b_x + \alpha_{x} * dev_x(t_{xi}) + b_{xt_{xi}} + b_i + b_{i,Bin(t_{xi})} \]
将模型2单独使用,可以获得RMSE=0.9505。
上面讨论中,电影偏差和用户无关,但是用户在不同时间对电影的偏差反应岁的hi不同的,如用户失恋时更倾向于自己主观判断,而心情好的时候更加顾及其他用户对此电影的看法。为此,引入电影偏差和时间有关的用户尺度\(c_x(t_{xi})\):
\[ b_{xi} = \mu + b_x + \alpha_{x} * dev_x(t_{xi}) + b_{xt_{xi}} + (b_i + b_{i,Bin(t_{xi})}) * c_x(t_{xi}) \]
这里,\(c_x(t_{xi}) = c_x + c_{xt}\),\(c_x\)是稳定的部分,\(c_{xt}\)为每日变化的部分。引入\(c_x(t_{xi})\)之后模型的预测误差从0.9605下降到0.9555。
模型3:引入频率
Netflix的数据集是在不同背景的情况下收集的,有来自Netflix邀请的用户对以往看过的电影评分,也有用户自发行为的评分,这些评分应该区别对待。可以通过用户在同一天内评分的电影数量进行区分。
设\(F_{xi}\)为用户x在时间\(t_{xi}\)内提供的评分数量,\(f_{xi}=\lfloor \log_a^{F_{xi}} \rfloor\)。\(f_{xi}\)虽然跟用户有关,但是Netflix数据集上的结果表明\(f_{xi}\)却和电影偏差有关系,而不是用户偏差。用户对很久以前的电影进行评分说明用户一直保持着自己的兴趣,对电影而言,它被观看之后很久才获得评分,说明用户对它特别喜欢或者特别讨厌。
在模型2的基础之上对其加强: \[ b_{xi} = \mu + b_x + \alpha_{x} * dev_x(t_{xi}) + b_{xt_{xi}} + (b_i + b_{i,Bin(t_{xi})}) * c_x(t_{xi}) + b_{if_{xi}} \] 模型3将预测误差从0.9555下降到0.9278。
3.2 矩阵分解(Matrix Factorization)
因子模型(Factor Model)假设用户的特征可以用若干因子进行描述,电影的特征也可以同样的因子描述,那么当用户的特征和电影的特征吻合时,此时该用户会对电影给予高分。因子模型通常也被称之为矩阵分解,而奇异值分解(Singular Value Decomposition,SVD)是一种常见的矩阵分解。 \[ R = U\sum V^T = Q * P^T \]
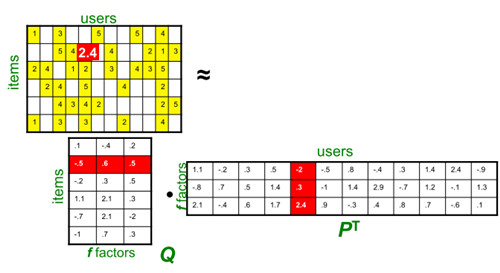
通过SVD分解为两个矩阵,分别为用户-因子矩阵和电影-因子矩阵。用户-因子矩阵中的因子表示用户的喜好,如偏女性还是偏男性、偏严肃还是偏喜剧等。电影-因子矩阵中的因子表示电影的类型,如喜剧片、爱情片等。
